On the interactive drawing the master principal ellipse has been placed at the correct altitude above sea level and the geometric construction from the south pole to the Stratopause that forms the passage step is shown highlighted in green.
The cursor display area of this programme has been amended and now shows altitude, in perfect meters, of the cursor's position relative to the Geoid's sea level at Giza. Move your cursor over the interactive drawing and you will see the live value of its altitude above sea level being displayed.
If you zoom in to the lower chamber you can see that the atmosphere geometry lines match the step in the lower chamber passage. This method for positioning the master ellipse is efficient because it resolves the X,Y and Z axis locations in one construction - the ellipsoid from which the ellipse is formed cannot move vertically on the Y axis or horizontally in either the X or Z directions without becoming detached from the step.
It is important to note that the master ellipse has just been placed on the lower chamber floor by taking measurements relative to sea level, and therefore the master ellipse has not been placed as part of the geometric structure, but as a derivation from that geometry - it is not part of the architectural geometry system.
With the master ellipse fixed in place it is possible to now determine how the scaling of the ellipse needs to be applied as the Earth moves from Perihelion to Aphelion in its orbit. You will recall that the scale of the model in use is 1:87,500 and if you position your cursor over the second horizontal lap of stone from the top on the niche carving in the lower chamber you will see that the altitude of this horizontal piece of the niche is 87.5 perfect meters above sea level. The niche has been constructed so that you can read off the Earth model scale from the altitude of its stone laps.
If you consider the Earth moving from Perihelion to Aphelion and take the median value, 1 AU, as the reference point at which the Earth has been scaled to a 1:87,500 model then you can determine the scale that would be required at Aphelion and Perihelion and compare those values to the altitudes of the niche's indentations.
To determine the scales it is necessary to understand the angles that are produced when the Earth is viewed from the Sun, which is termed 'angular diameter' by astronomers and an explanation of the concept can be found here. The following illustration shows the Earth at Perihelion and Aphelion and includes the distances and angles required to calculate the apparent diameter of the planet when viewed from the Sun.
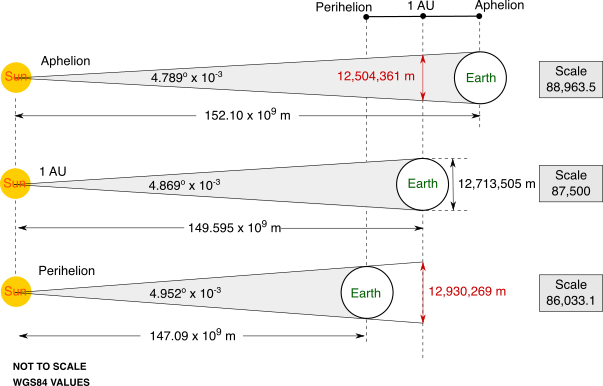
If you work out the angular diameter of the Earth when viewed from the Sun when the Earth is at Perihelion and Aphelion and then calculate the angular diameter relative to the Earth when it is at 1 AU position you can deduce that, in order to keep the ellipse a constant size, then the scale of the model required at Aphelion would be 1:88,963.5 and at Perihelion 1:86,033.1. If you move your cursor over the niche carving you will see that these values are replicated in the horizontal sections of stone, and if you click here you can overlay an explanatory graphic showing the sea level altitudes of the niche that correspond to the scales.
As the illustration shows, the altitude lines do not coincide exactly with the niche horizontal levels and therefore a calibration is required for this system.