The lower northern shaft cannot be solved in this basic geometric system because further information is required before its design system can be deduced. It is solved in the next section of this work. All that is known about the shaft at this stage is that its lower section has an angle of approximately 40°, and that neither of the engineering teams who surveyed the shaft could get a accurate value for the its angle.
It is important to note that the measurements of this shaft's length reported by the 1993 robotics survey 'Upuaut' do not correspond to the results obtained by the more accurate later survey of the 'Djedi project'. The measurements used in this work for the lower southern shaft are taken from original raw data measurements which were kindly provided to me by the engineering team of the later survey. The length of the stonework in the angled section of this shaft is 61.5 m.
Click here to zoom in on the lower southern shaft area.
The lower southern shaft is formed in the following manner (mouse over the bullet points to show the geometric feature):
If you click here you can see that the angle of the geometric line that is formed in this manner is very close to the surveyed angle of the lower southern shaft and the geometric line is also located inside the confines of the shaft's walls.
The only way that the length of this shaft line can be determined is by using the lessons learned in the gallery, and therefore by multiplying its angle in radians by 200 to get its cubit length. The geometric line that is shown on the drawing is constructed in this manner, and is quite clearly is nowhere near the surveyed length of the shaft. However if you click here (click and hold) to zoom in on the top section of the shaft you can see that at the point where you would expect the shaft to terminate, the architects have built a drop into the floor's stonework. ( This floor drop caused large problems for the robotics surveying , and was nicknamed "the tank trap" by the team of engineers. The original report can be found on the team's website.)
At the top of this shaft is a blocking stone which is known as "Gantenbrink's door" after the lead engineer of the surveying team who discovered it. During subsequent robotics explorations of this shaft by The Djedi Project of Leeds University in the UK, the door was drilled through and a micro-camera and a light were inserted through the hole to photograph the small cavity that lies behind the door. The images obtained were published in The New Scientist and below is an enhanced image of the hieratic symbols that were found behind the door. (The hieratic symbol chart is adapted from an original on St Andrew's university website.)
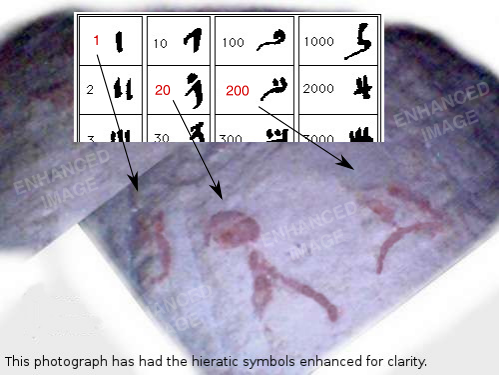
Written behind the door is the number 221.
This number is the correct cubit to radian ratio of the shaft and if you click here the construction methodology of the lower southern shaft is displayed. The shaft has 'two lengths', the first is to the dropped floor stone at 200 cubits to the radian, and the second is to the end of the shaft behind the door at 221 cubits to the radian. These two integer values, 221 and 200, are invaluable for fully understanding the gallery later in this work.
The angle of this geometric shaft line can be seen in the object information panel for the lower southern shaft. The geometric angle is 39.52517° and the surveyed angle is 39.6078° ± 0.1°. The geometric shaft angle is nearly one tenth of a degree lower than that of the surveyed angle, which is at the outer margins of the surveying tolerance. However, from the movable geometry of the ascending passage seen earlier (page B7), the architects have already shown how to adjust the geometry for non-matching angles in the construction - by rotating the Earth ellipses.