The interactive drawing shows a newly created master ellipse highlighted in green and this is the ellipse that is being created from an orthographic projection of the Earth as viewed from the Sun. The large white ellipse that is the same size as the master ellipse but is rotating at half the frequency of the master ellipse is the principal geometry ellipse, and the secondary ellipse at the bottom of the pyramid has also been geared so that it is rotating at half the frequency of the master ellipse. The master ellipse is using the same center point as the principal ellipse.
If you zoom in to the key plot area and let the plot develop you can see that the left side of the key is now plotting correctly with the blue and yellow plots running along the same curved line.
There is however one further problem with the astronomy that is associated with the geometry on the screen. If the projection onto the gallery floor represents the movement of the Earth between Perihelion and Aphelion then on the right side of the plot ,when the Earth is at Perihelion, you would expect the angular velocity of the Earth around the Sun be at its maximum and that the curved key line and the straight projection line would meet at this point. As you can see this is not the case.
The solution to this problem is to project the curved plot onto a line which is perpendicular to the tangent of that curved plot at its end point. This does not need solving with fresh mathematics because the curved key plot is simply the hexagonal rod rotated and reflected and therefore the straight section of the hexagonal rod must have been the tangent line to the curved part of the hexagonal rod before the rotation and reflection took place, since originally the rod was one continuous plot until the gearing removed the straight section from the geometry.
To create a geometric line onto which the curved key can be plotted requires reflecting the hexagonal rod in a vertical line that passes through the point at the top of the rod's straight section, and then taking a perpendicular to the reflected rod which starts at the top point of the straight section of rod. You can display this geometry on the interactive drawing. The two highlighted green lines are at right angles to each other, the green line on the right is a reflection of the hexagonal rod, and the green line on the left is the perpendicular to the reflected rod onto which the dynamic key plot can now be projected.
You can remove the projection from the gallery floor and instead project the key onto the newly created perpendicular rod reflection line by clicking here.
The movement of the Earth from Perihelion to Aphelion is now represented by this new projection, and the length of the projection line that is created by the dynamic geometry is 5.99 cubits in length. The value of the Earth's distance from the Sun at any moment during its annual orbit can be read off from this scale, if the nominal length of the line is supposed to be exactly 6 cubits, by measuring the distance from the top of the hexagonal rod's straight section to the projection point.
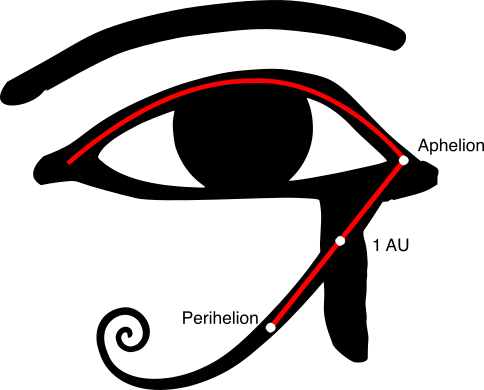
It does not take that much artistic imagination to look at the dynamic geometry plot on the screen, and to compare it to one of the most iconic hieroglyph symbols from ancient Egypt, the Eye of Horus, to see where the symbol has originated from. The 'tear' that comes vertically from the 'eye' marks off the mid point between Aphelion and Perihelion which is the fundamental measure of distance used by astronomers called the astronomical unit, or 1 AU, the median distance of the Earth from the Sun during the year.